The code currently uses SymPy, but should be possible to convert to Sage's symbolics (it mostly requires basic pattern matching, and evaluation of standard special functions). Perhaps "rewrite" is a better word than "convert" because the current code is a messy hack. It's buggy, and only handles special cases in places where a general approach could be used (such as for rational functions).
The basic idea behind the code is to perform the evaluation in two steps. Firstly, the given series is converted into canonical form. I've used the standard generalized hypergeometric series pFq. This is not always an optimal representation, but usually does the job.
In the second step, parameter transformations and table lookups are used to reduce the pFq series into elementary (or simpler) functions when possible. If this step fails, the pFq function is returned, giving a closed-form solution that can be manipulated or evaluated numerically.
The second step is the most difficult, because the transformation algorithms that need to be used for hypergeometric functions are very complicated in general (and there are all kinds of special cases). So far I've only implemented some simple transformations. For the final lookup stage, it would be straightforward to also implement expansion into Bessel functions, incomplete gamma functions, etc.
Below is a sample of some working test cases, with numerical evaluation of both the evaluated result and the original series as verification. Some of the sums don't quite simplify fully, i.e. there is an unevaluated pFq function left. The formulas were mostly generated with SymPy's latex function, so they are not always as pretty as could be.
![\sum_{k=0}^{\infty} k!^{-1} = e [; \sum_{k=0}^{\infty} k!^{-1} = e ;]](http://fredrikj.net/blah/gif_034.gif)
>>> hypsum(1 / fac(k), k)
E
>>> _.evalf()
2.71828182845905
>>> mpmath.nsum(lambda k: 1 / mpmath.fac(k), [0,mpmath.inf])
2.71828182845905
![\sum_{k=0}^{\infty} \frac{k^{6}}{k!} = 203 e [; \sum_{k=0}^{\infty} \frac{k^{6}}{k!} = 203 e ;]](http://fredrikj.net/blah/gif_031.gif)
>>> hypsum(k**6 / fac(k), k)
203*E
>>> _.evalf()
551.811211177186
>>> mpmath.nsum(lambda k: k**6 / mpmath.fac(k), [0,mpmath.inf])
551.811211177186
![\sum_{k=0}^{\infty} 4 \frac{d k z^{2 + k}}{k!} = 4 d z^{3} e^{z} [; \sum_{k=0}^{\infty} 4 \frac{d k z^{2 + k}}{k!} = 4 d z^{3} e^{z} ;]](http://fredrikj.net/blah/gif_012.gif)
>>> hypsum(4 * d * k * z**(k+2) / fac(k), k)
4*d*z**3*exp(z)
>>> _.evalf(subs={d:'1/2',z:'1/4'})
0.0401257942714919
>>> mpmath.nsum(lambda k: 4 * 0.5 * k * 0.25**(k+2) / mpmath.fac(k), [0,mpmath.inf])
0.0401257942714919
![\sum_{k=0}^{\infty} \left({\left(2\right)}_{k}\right)^{-1} = -1 + e [; \sum_{k=0}^{\infty} \left({\left(2\right)}_{k}\right)^{-1} = -1 + e ;]](http://fredrikj.net/blah/gif_010.gif)
>>> hypsum(1 / rf(2,k), k)
-1 + E
>>> _.evalf()
1.71828182845905
>>> mpmath.nsum(lambda k: 1 / mpmath.rf(2,k), [0,mpmath.inf])
1.71828182845905
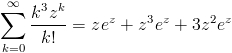
>>> simplify(hypsum(k**3 * z**(k) / fac(k), k))
z*exp(z) + z**3*exp(z) + 3*z**2*exp(z)
>>> _.evalf(subs={d:'1/2',z:'1/4'})
0.581824016936633
>>> mpmath.nsum(lambda k: k**3 * 0.25**(k) / mpmath.fac(k), [0,mpmath.inf])
0.581824016936633
![\sum_{k=0}^{\infty} {{2 k}\choose{k}}^{-1} = \frac{4}{3} + \frac{2}{27} \pi \sqrt{3} [; \sum_{k=0}^{\infty} {{2 k}\choose{k}}^{-1} = \frac{4}{3} + \frac{2}{27} \pi \sqrt{3} ;]](http://fredrikj.net/blah/gif_035.gif)
>>> simplify(hypsum(1 / binomial(2*k,k), k))
4/3 + 2*pi*3**(1/2)/27 >>> _.evalf()
1.73639985871872
>>> mpmath.nsum(lambda k: 1 / mpmath.binomial(2*k,k), [0,mpmath.inf])
1.73639985871872
![\sum_{k=0}^{\infty} {{3 k}\choose{k}}^{-1} = \frac{2}{3} \frac{\pi \sqrt{3} \,_{3}F_{2}\left(\frac{1}{2},1,1; \frac{1}{3},\frac{2}{3}; \frac{4}{27}\right)}{\operatorname{\Gamma}\left(\frac{1}{3}\right) \operatorname{\Gamma}\left(\frac{2}{3}\right)} [; \sum_{k=0}^{\infty} {{3 k}\choose{k}}^{-1} = \frac{2}{3} \frac{\pi \sqrt{3} \,_{3}F_{2}\left(\frac{1}{2},1,1; \frac{1}{3},\frac{2}{3}; \frac{4}{27}\right)}{\operatorname{\Gamma}\left(\frac{1}{3}\right) \operatorname{\Gamma}\left(\frac{2}{3}\right)} ;]](http://fredrikj.net/blah/gif_019.gif)
>>> hypsum(1 / binomial(3*k,k), k)
2*pi*3**(1/2)*3F2([1/2, 1, 1], [1/3, 2/3], 4/27)/(3*gamma(1/3)*gamma(2/3))
>>> _.evalf()
1.41432204432182
>>> mpmath.nsum(lambda k: 1 / mpmath.binomial(3*k,k), [0,mpmath.inf])
1.41432204432182
![\sum_{k=0}^{\infty} \frac{k^{4}}{{{2 k}\choose{k}}} = \frac{32}{3} + \frac{238}{243} \pi \sqrt{3} [; \sum_{k=0}^{\infty} \frac{k^{4}}{{{2 k}\choose{k}}} = \frac{32}{3} + \frac{238}{243} \pi \sqrt{3} ;]](http://fredrikj.net/blah/gif_002.gif)
>>> hypsum(k**4 / binomial(2*k,k), k)
32/3 + 238*pi*3**(1/2)/243
>>> _.evalf()
15.9961018356512
>>> mpmath.nsum(lambda k: k**4 / mpmath.binomial(2*k,k), [0,mpmath.inf])
15.9961018356512
![\sum_{k=0}^{\infty} \frac{\left(1 + k\right)! \left(2 + k\right)!}{\left(3 + k\right)! \left(4 + k\right)!} = \frac{1}{72} \,_{3}F_{2}\left(1,2,3; 4,5; 1\right) [; \sum_{k=0}^{\infty} \frac{\left(1 + k\right)! \left(2 + k\right)!}{\left(3 + k\right)! \left(4 + k\right)!} = \frac{1}{72} \,_{3}F_{2}\left(1,2,3; 4,5; 1\right) ;]](http://fredrikj.net/blah/gif_005.gif)
>>> hypsum(fac(k+1)*fac(k+2)/fac(k+3)/fac(k+4), k)
3F2([1, 2, 3], [4, 5], 1)/72
>>> _.evalf()
0.0217325998184402
>>> mpmath.nsum(lambda k: mpmath.fac(k+1)*mpmath.fac(k+2)/mpmath.fac(k+3)/mpmath.fac(k+4), [0,mpmath.inf])
0.0217325998184402
![\sum_{k=0}^{\infty} \frac{1}{\left(3 + k\right)^{2} \left(8 + 6 k + k^{2}\right)} = \frac{1}{72} \,_{3}F_{2}\left(1,2,3; 4,5; 1\right) [; \sum_{k=0}^{\infty} \frac{1}{\left(3 + k\right)^{2} \left(8 + 6 k + k^{2}\right)} = \frac{1}{72} \,_{3}F_{2}\left(1,2,3; 4,5; 1\right) ;]](http://fredrikj.net/blah/gif_028.gif)
>>> hypsum(1/((3+k)**2*(8+6*k+k**2)), k)
3F2([1, 2, 3], [4, 5], 1)/72
>>> _.evalf()
0.0217325998184402
>>> mpmath.nsum(lambda k: 1/((3+k)**2*(8+6*k+k**2)), [0,mpmath.inf])
0.0217325998184402
![\sum_{k=0}^{\infty} \frac{\left(1 + 2 k\right)!}{\left(1 + k\right) \left(2 + 2 k\right)!} = \frac{1}{12} \pi^{2} [; \sum_{k=0}^{\infty} \frac{\left(1 + 2 k\right)!}{\left(1 + k\right) \left(2 + 2 k\right)!} = \frac{1}{12} \pi^{2} ;]](http://fredrikj.net/blah/gif_025.gif)
>>> hypsum(fac(2*k+1)/(fac(2*k+2)*(k+1)), k)
pi**2/12
>>> _.evalf()
0.822467033424113
>>> mpmath.nsum(lambda k: mpmath.fac(2*k+1)/(mpmath.fac(2*k+2)*(k+1)), [0,mpmath.inf])
0.822467033424113
![\sum_{k=0}^{\infty} \frac{\left(1 + 2 k\right)!}{\left(2 + 3 k\right)!} = \frac{2}{27} \frac{\pi \sqrt{3} \,_{2}F_{2}\left(1,\frac{3}{2}; \frac{4}{3},\frac{5}{3}; \frac{4}{27}\right)}{\operatorname{\Gamma}\left(\frac{4}{3}\right) \operatorname{\Gamma}\left(\frac{5}{3}\right)} [; \sum_{k=0}^{\infty} \frac{\left(1 + 2 k\right)!}{\left(2 + 3 k\right)!} = \frac{2}{27} \frac{\pi \sqrt{3} \,_{2}F_{2}\left(1,\frac{3}{2}; \frac{4}{3},\frac{5}{3}; \frac{4}{27}\right)}{\operatorname{\Gamma}\left(\frac{4}{3}\right) \operatorname{\Gamma}\left(\frac{5}{3}\right)} ;]](http://fredrikj.net/blah/gif_023.gif)
>>> hypsum(fac(2*k+1)/(fac(3*k+2)), k)
2*pi*3**(1/2)*2F2([1, 3/2], [4/3, 5/3], 4/27)/(27*gamma(4/3)*gamma(5/3))
>>> _.evalf()
0.553106730441975
>>> mpmath.nsum(lambda k: mpmath.fac(2*k+1)/(mpmath.fac(3*k+2)), [0,mpmath.inf])
0.553106730441975
![\sum_{k=0}^{\infty} \frac{4^{k} \left(\frac{3}{2} + k\right)! \left(\frac{5}{2} + k\right)!}{\left(6 + 2 k\right)!} = \frac{3}{256} \pi [; \sum_{k=0}^{\infty} \frac{4^{k} \left(\frac{3}{2} + k\right)! \left(\frac{5}{2} + k\right)!}{\left(6 + 2 k\right)!} = \frac{3}{256} \pi ;]](http://fredrikj.net/blah/gif_013.gif)
>>> hypsum(4**k*fac(k+R32)*fac(k+R52)/(fac(2*k+6)), k)
3*pi/256
>>> _.evalf()
0.0368155389092554
>>> mpmath.nsum(lambda k: 4**k*mpmath.fac(k+1.5)*mpmath.fac(k+2.5)/(mpmath.fac(2*k+6)), [0,mpmath.inf], method='e')
0.0368155389092358
![\sum_{k=0}^{\infty} \frac{\left(-1\right)^{k} z^{1 + 2 k}}{\left(1 + 2 k\right) k!} = \frac{1}{2} \sqrt{\pi} \operatorname{erf}\left(z\right) [; \sum_{k=0}^{\infty} \frac{\left(-1\right)^{k} z^{1 + 2 k}}{\left(1 + 2 k\right) k!} = \frac{1}{2} \sqrt{\pi} \operatorname{erf}\left(z\right) ;]](http://fredrikj.net/blah/gif_027.gif)
>>> hypsum((-1)**k * z**(2*k+1) / fac(k) / (2*k+1), k)
pi**(1/2)*erf(z)/2
>>> _.evalf(subs={d:'1/2',z:'1/4'})
0.244887887180256
>>> mpmath.nsum(lambda k: (-1)**k * 0.25**(2*k+1) / mpmath.fac(k) / (2*k+1), [0,mpmath.inf])
0.244887887180256
![\sum_{k=0}^{\infty} \frac{z^{1 + 2 k}}{1 + 2 k} = \operatorname{atanh}\left(z\right) [; \sum_{k=0}^{\infty} \frac{z^{1 + 2 k}}{1 + 2 k} = \operatorname{atanh}\left(z\right) ;]](http://fredrikj.net/blah/gif_011.gif)
>>> hypsum(z**(2*k+1) / (2*k+1), k)
atanh(z)
>>> _.evalf(subs={d:'1/2',z:'1/4'})
0.255412811882995
>>> mpmath.nsum(lambda k: 0.25**(2*k+1) / (2*k+1), [0,mpmath.inf])
0.255412811882995
![\sum_{k=0}^{\infty} \frac{z^{k}}{1 + 2 k} = \frac{\operatorname{atanh}\left(\sqrt{z}\right)}{\sqrt{z}} [; \sum_{k=0}^{\infty} \frac{z^{k}}{1 + 2 k} = \frac{\operatorname{atanh}\left(\sqrt{z}\right)}{\sqrt{z}} ;]](http://fredrikj.net/blah/gif_037.gif)
>>> hypsum(z**k / (2*k+1), k)
atanh(z**(1/2))/z**(1/2)
>>> _.evalf(subs={d:'1/2',z:'1/4'})
1.09861228866811
>>> mpmath.nsum(lambda k: 0.25**k / (2*k+1), [0,mpmath.inf])
1.09861228866811
![\sum_{k=0}^{\infty} \frac{\left(- z\right)^{k}}{1 + k} = \frac{\operatorname{log}\left(1 + z\right)}{z} [; \sum_{k=0}^{\infty} \frac{\left(- z\right)^{k}}{1 + k} = \frac{\operatorname{log}\left(1 + z\right)}{z} ;]](http://fredrikj.net/blah/gif_032.gif)
>>> hypsum((-z)**k / (k+1), k)
log(1 + z)/z
>>> _.evalf(subs={d:'1/2',z:'1/4'})
0.892574205256839
>>> mpmath.nsum(lambda k: (-0.25)**k / (k+1), [0,mpmath.inf])
0.892574205256839
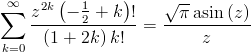
>>> hypsum(fac(k-R12)/((1+2*k)*fac(k))*z**(2*k), k)
pi**(1/2)*asin(z)/z
>>> _.evalf(subs={d:'1/2',z:'1/4'})
1.79145636509746
>>> mpmath.nsum(lambda k: mpmath.fac(k-0.5)/((1+2*k)*mpmath.fac(k))*0.25**(2*k), [0,mpmath.inf])
1.79145636509746
![\sum_{k=0}^{\infty} \frac{z^{k}}{\left(2 + k\right)!} = - \frac{1 + z - e^{z}}{z^{2}} [; \sum_{k=0}^{\infty} \frac{z^{k}}{\left(2 + k\right)!} = - \frac{1 + z - e^{z}}{z^{2}} ;]](http://fredrikj.net/blah/gif_018.gif)
>>> hypsum(z**k / fac(k+2), k)
-(1 + z - exp(z))/z**2
>>> _.evalf(subs={d:'1/2',z:'1/4'})
0.544406667003864
>>> mpmath.nsum(lambda k: 0.25**k / mpmath.fac(k+2), [0,mpmath.inf])
0.544406667003864
![\sum_{k=0}^{\infty} \left(-5 + 3 z^{2}\right)^{3 - 4 k} = - \frac{\left(5 - 3 z^{2}\right)^{3}}{1 - \frac{1}{\left(5 - 3 z^{2}\right)^{4}}} [; \sum_{k=0}^{\infty} \left(-5 + 3 z^{2}\right)^{3 - 4 k} = - \frac{\left(5 - 3 z^{2}\right)^{3}}{1 - \frac{1}{\left(5 - 3 z^{2}\right)^{4}}} ;]](http://fredrikj.net/blah/gif_014.gif)
>>> hypsum((3*z**2-5)**(-4*k+3), k)
-(5 - 3*z**2)**3/(1 - 1/(5 - 3*z**2)**4)
>>> _.evalf(subs={d:'1/2',z:'1/4'})
-111.666432272586
>>> mpmath.nsum(lambda k: (3*0.25**2-5)**(-4*k+3), [0,mpmath.inf])
-111.666432272586
![\sum_{k=0}^{\infty} \frac{z^{1 + 2 k}}{\left(1 + 2 k\right)!} = \operatorname{sinh}\left(z\right) [; \sum_{k=0}^{\infty} \frac{z^{1 + 2 k}}{\left(1 + 2 k\right)!} = \operatorname{sinh}\left(z\right) ;]](http://fredrikj.net/blah/gif_016.gif)
>>> hypsum(z**(2*k+1) / fac(2*k+1), k)
sinh(z)
>>> _.evalf(subs={d:'1/2',z:'1/4'})
0.252612316808168
>>> mpmath.nsum(lambda k: 0.25**(2*k+1) / mpmath.fac(2*k+1), [0,mpmath.inf])
0.252612316808168
![\sum_{k=0}^{\infty} \frac{\left(-1\right)^{k} z^{1 + 2 k}}{\left(1 + 2 k\right)!} = \operatorname{sin}\left(z\right) [; \sum_{k=0}^{\infty} \frac{\left(-1\right)^{k} z^{1 + 2 k}}{\left(1 + 2 k\right)!} = \operatorname{sin}\left(z\right) ;]](http://fredrikj.net/blah/gif_022.gif)
>>> hypsum((-1)**k * z**(2*k+1) / fac(2*k+1), k)
sin(z)
>>> _.evalf(subs={d:'1/2',z:'1/4'})
0.247403959254523
>>> mpmath.nsum(lambda k: (-1)**k * 0.25**(2*k+1) / mpmath.fac(2*k+1), [0,mpmath.inf])
0.247403959254523
![\sum_{k=0}^{\infty} \frac{\left(-1\right)^{k} d^{k} \left(1 - z\right)^{1 + 2 k}}{\left(2 k\right)!} = \left(1 - z\right) \operatorname{cos}\left(\sqrt{d} \left(1 - z\right)\right) [; \sum_{k=0}^{\infty} \frac{\left(-1\right)^{k} d^{k} \left(1 - z\right)^{1 + 2 k}}{\left(2 k\right)!} = \left(1 - z\right) \operatorname{cos}\left(\sqrt{d} \left(1 - z\right)\right) ;]](http://fredrikj.net/blah/gif_038.gif)
>>> hypsum((-1)**k * d**k * (1-z)**(2*k+1) / fac(2*k), k)
(1 - z)*cos(d**(1/2)*(1 - z))
>>> _.evalf(subs={d:'1/2',z:'1/4'})
0.646980115568008
>>> mpmath.nsum(lambda k: (-1)**k * 0.5**k * (1-0.25)**(2*k+1) / mpmath.fac(2*k), [0,mpmath.inf])
0.646980115568008
![\sum_{k=0}^{\infty} \frac{k z^{2 k}}{\left(1 + 2 k\right)!} = \frac{1}{2} \operatorname{cosh}\left(z\right) - \frac{\operatorname{sinh}\left(z\right)}{2 z} [; \sum_{k=0}^{\infty} \frac{k z^{2 k}}{\left(1 + 2 k\right)!} = \frac{1}{2} \operatorname{cosh}\left(z\right) - \frac{\operatorname{sinh}\left(z\right)}{2 z} ;]](http://fredrikj.net/blah/gif_007.gif)
>>> hypsum(k * z**(2*k) / fac(2*k+1), k)
cosh(z)/2 - sinh(z)/(2*z)
>>> _.evalf(subs={d:'1/2',z:'1/4'})
0.0104819163234500
>>> mpmath.nsum(lambda k: k * 0.25**(2*k) / mpmath.fac(2*k+1), [0,mpmath.inf])
0.01048191632345
![\sum_{k=0}^{\infty} \frac{\operatorname{\Gamma}^{2}\left(- \frac{1}{2} + k\right)}{k!^{2}} = 16 [; \sum_{k=0}^{\infty} \frac{\operatorname{\Gamma}^{2}\left(- \frac{1}{2} + k\right)}{k!^{2}} = 16 ;]](http://fredrikj.net/blah/gif_020.gif)
>>> hypsum(gamma(k-R12)**2/(fac(k)**2), k)
16
>>> _.evalf()
16.0000000000000
>>> mpmath.nsum(lambda k: mpmath.gamma(k-0.5)**2/(mpmath.fac(k)**2), [0,mpmath.inf])
16.0
![\sum_{k=0}^{\infty} \left(1 + k\right)^{-2} = \frac{1}{6} \pi^{2} [; \sum_{k=0}^{\infty} \left(1 + k\right)^{-2} = \frac{1}{6} \pi^{2} ;]](http://fredrikj.net/blah/gif_029.gif)
>>> hypsum(1/(k+1)**2, k)
pi**2/6
>>> _.evalf()
1.64493406684823
>>> mpmath.nsum(lambda k: 1/(k+1)**2, [0,mpmath.inf])
1.64493406684823
![\sum_{k=0}^{\infty} \frac{k}{\left(1 + k\right)^{3}} = - \operatorname{\zeta}\left(3\right) + \frac{1}{6} \pi^{2} [; \sum_{k=0}^{\infty} \frac{k}{\left(1 + k\right)^{3}} = - \operatorname{\zeta}\left(3\right) + \frac{1}{6} \pi^{2} ;]](http://fredrikj.net/blah/gif_004.gif)
>>> hypsum(k/(k+1)**3, k)
-zeta(3) + pi**2/6
>>> _.evalf()
0.442877163688632
>>> mpmath.nsum(lambda k: k/(k+1)**3, [0,mpmath.inf])
0.442877163688632
![\sum_{k=0}^{\infty} \frac{z^{k} \left(3 + k\right)}{\left(3 + 3 k\right) k!} = - \frac{2 - 2 e^{z} - z e^{z}}{3 z} [; \sum_{k=0}^{\infty} \frac{z^{k} \left(3 + k\right)}{\left(3 + 3 k\right) k!} = - \frac{2 - 2 e^{z} - z e^{z}}{3 z} ;]](http://fredrikj.net/blah/gif_015.gif)
>>> simplify(hypsum((3+k)/(3+3*k)*z**k/fac(k), k))
-(2 - 2*exp(z) - z*exp(z))/(3*z)
>>> _.evalf(subs={d:'1/2',z:'1/4'})
1.18540958339656
>>> mpmath.nsum(lambda k: (3+k)/(3+3*k)*0.25**k/mpmath.fac(k), [0,mpmath.inf])
1.18540958339656
![\sum_{k=0}^{\infty} \frac{k^{2} z^{1 + 2 k}}{\left(9 + 2 k\right)!} = \frac{1}{39916800} z^{3} \left(- \,_{1}F_{2}\left(2; 6,\frac{13}{2}; \frac{1}{4} z^{2}\right) + 2 \,_{1}F_{2}\left(3; 6,\frac{13}{2}; \frac{1}{4} z^{2}\right)\right) [; \sum_{k=0}^{\infty} \frac{k^{2} z^{1 + 2 k}}{\left(9 + 2 k\right)!} = \frac{1}{39916800} z^{3} \left(- \,_{1}F_{2}\left(2; 6,\frac{13}{2}; \frac{1}{4} z^{2}\right) + 2 \,_{1}F_{2}\left(3; 6,\frac{13}{2}; \frac{1}{4} z^{2}\right)\right) ;]](http://fredrikj.net/blah/gif_003.gif)
>>> hypsum(k**2 * z**(2*k+1) / fac(2*k+9), k)
z**3*(-1F2([2], [6, 13/2], z**2/4) + 2*1F2([3], [6, 13/2], z**2/4))/39916800
>>> _.evalf(subs={d:'1/2',z:'1/4'})
3.92066920165299e-10
>>> mpmath.nsum(lambda k: k**2 * 0.25**(2*k+1) / mpmath.fac(2*k+9), [0,mpmath.inf])
3.92066920165299e-10
![\sum_{k=0}^{\infty} z^{k} \left(1 + k\right) \left(1 + 2 k\right) \left(2 + k\right) \left(3 + k\right) = \frac{6 + 42 z}{1 - 5 z + 10 z^{2} - 10 z^{3} + 5 z^{4} - z^{5}} [; \sum_{k=0}^{\infty} z^{k} \left(1 + k\right) \left(1 + 2 k\right) \left(2 + k\right) \left(3 + k\right) = \frac{6 + 42 z}{1 - 5 z + 10 z^{2} - 10 z^{3} + 5 z^{4} - z^{5}} ;]](http://fredrikj.net/blah/gif_041.gif)
>>> simplify(hypsum((k+1)*(k+2)*(k+3)*(1+2*k)*z**k, k))
(6 + 42*z)/(1 - 5*z + 10*z**2 - 10*z**3 + 5*z**4 - z**5)
>>> _.evalf(subs={d:'1/2',z:'1/4'})
69.5308641975309
>>> mpmath.nsum(lambda k: (k+1)*(k+2)*(k+3)*(1+2*k)*0.25**k, [0,mpmath.inf])
69.5308641975309
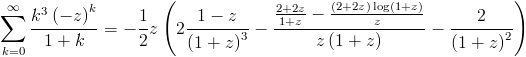
>>> hypsum(k**3 * (-z)**k / (k+1), k)
-z*(2*(1 - z)/(1 + z)**3 - ((2 + 2*z)/(1 + z) - (2 + 2*z)*log(1 + z)/z)/(z*(1 + z)) - 2/(1 + z)**2)/2
>>> _.evalf(subs={d:'1/2',z:'1/4'})
-0.0285742052568390
>>> mpmath.nsum(lambda k: k**3 * (-0.25)**k / (k+1), [0,mpmath.inf])
-0.028574205256839
![\sum_{k=0}^{\infty} \frac{e^{k}}{k!} = e^{e} [; \sum_{k=0}^{\infty} \frac{e^{k}}{k!} = e^{e} ;]](http://fredrikj.net/blah/gif_017.gif)
>>> hypsum(E**k / fac(k), k)
exp(E)
>>> _.evalf()
15.1542622414793
>>> mpmath.nsum(lambda k: mpmath.e**k / mpmath.fac(k), [0,mpmath.inf])
15.1542622414793
![\sum_{k=0}^{\infty} \frac{\operatorname{cos}\left(k\right)}{k!} = \frac{1}{2} e^{e^{\mathbf{\imath}}} + \frac{1}{2} e^{e^{- \mathbf{\imath}}} [; \sum_{k=0}^{\infty} \frac{\operatorname{cos}\left(k\right)}{k!} = \frac{1}{2} e^{e^{\mathbf{\imath}}} + \frac{1}{2} e^{e^{- \mathbf{\imath}}} ;]](http://fredrikj.net/blah/gif_033.gif)
>>> hypsum(cos(k) / fac(k), k)
exp(exp(I))/2 + exp(exp(-I))/2
>>> _.evalf()
1.14383564379164 + .0e-20*I
>>> mpmath.nsum(lambda k: mpmath.cos(k) / mpmath.fac(k), [0,mpmath.inf])
1.14383564379164
![\sum_{k=0}^{\infty} \frac{\operatorname{cos}\left(k\right)}{1 + 2 k} = \frac{1}{2} \operatorname{atanh}\left(e^{- \frac{1}{2} \mathbf{\imath}}\right) e^{\frac{1}{2} \mathbf{\imath}} + \frac{1}{2} \operatorname{atanh}\left(e^{\frac{1}{2} \mathbf{\imath}}\right) e^{- \frac{1}{2} \mathbf{\imath}} [; \sum_{k=0}^{\infty} \frac{\operatorname{cos}\left(k\right)}{1 + 2 k} = \frac{1}{2} \operatorname{atanh}\left(e^{- \frac{1}{2} \mathbf{\imath}}\right) e^{\frac{1}{2} \mathbf{\imath}} + \frac{1}{2} \operatorname{atanh}\left(e^{\frac{1}{2} \mathbf{\imath}}\right) e^{- \frac{1}{2} \mathbf{\imath}} ;]](http://fredrikj.net/blah/gif_024.gif)
>>> hypsum(cos(k) / (2*k+1), k)
atanh(exp(-I/2))*exp(I/2)/2 + atanh(exp(I/2))*exp(-I/2)/2
>>> _.evalf()
0.975556628913311
>>> mpmath.nsum(lambda k: mpmath.cos(k) / (2*k+1), [0,mpmath.inf])
0.975556628913311
![\sum_{k=0}^{\infty} \frac{k \operatorname{cos}\left(k\right)}{k!} = \frac{1}{2} e^{\mathbf{\imath} + e^{\mathbf{\imath}}} + \frac{1}{2} e^{- \mathbf{\imath} + e^{- \mathbf{\imath}}} [; \sum_{k=0}^{\infty} \frac{k \operatorname{cos}\left(k\right)}{k!} = \frac{1}{2} e^{\mathbf{\imath} + e^{\mathbf{\imath}}} + \frac{1}{2} e^{- \mathbf{\imath} + e^{- \mathbf{\imath}}} ;]](http://fredrikj.net/blah/gif_036.gif)
>>> simplify(hypsum(cos(k) * k / fac(k), k))
exp(I + exp(I))/2 + exp(-I + exp(-I))/2
>>> _.evalf()
-0.458967373729452 + .0e-20*I
>>> mpmath.nsum(lambda k: mpmath.cos(k) * k / mpmath.fac(k), [0,mpmath.inf])
-0.458967373729452
![\sum_{k=0}^{\infty} \frac{\left(-1\right)^{k}}{1 + 2 k} = \frac{1}{4} \pi [; \sum_{k=0}^{\infty} \frac{\left(-1\right)^{k}}{1 + 2 k} = \frac{1}{4} \pi ;]](http://fredrikj.net/blah/gif_009.gif)
>>> hypsum((-1)**k / (2*k+1), k)
pi/4
>>> _.evalf()
0.785398163397448
>>> mpmath.nsum(lambda k: (-1)**k / (2*k+1), [0,mpmath.inf])
0.785398163397448
![\sum_{k=0}^{\infty} \frac{\left(-1\right)^{k}}{6 + 2 k} = - \frac{1}{4} + \frac{1}{2} \operatorname{log}\left(2\right) [; \sum_{k=0}^{\infty} \frac{\left(-1\right)^{k}}{6 + 2 k} = - \frac{1}{4} + \frac{1}{2} \operatorname{log}\left(2\right) ;]](http://fredrikj.net/blah/gif_006.gif)
>>> hypsum((-1)**k / (2*k+6), k)
-1/4 + log(2)/2
>>> _.evalf()
0.0965735902799727
>>> mpmath.nsum(lambda k: (-1)**k / (2*k+6), [0,mpmath.inf])
0.0965735902799727
![\sum_{k=0}^{\infty} \frac{\left(-1\right)^{k}}{\left(1 + 2 k\right)^{2}} = C [; \sum_{k=0}^{\infty} \frac{\left(-1\right)^{k}}{\left(1 + 2 k\right)^{2}} = C ;]](http://fredrikj.net/blah/gif_040.gif)
>>> hypsum((-1)**k / (2*k+1)**2, k)
Catalan
>>> _.evalf()
0.915965594177219
>>> mpmath.nsum(lambda k: (-1)**k / (2*k+1)**2, [0,mpmath.inf])
0.915965594177219
![\sum_{k=0}^{\infty} \frac{\left(-1\right)^{k}}{\left(2 + 2 k\right)^{2}} = \frac{1}{48} \pi^{2} [; \sum_{k=0}^{\infty} \frac{\left(-1\right)^{k}}{\left(2 + 2 k\right)^{2}} = \frac{1}{48} \pi^{2} ;]](http://fredrikj.net/blah/gif_030.gif)
>>> hypsum((-1)**k / (2*k+2)**2, k)
pi**2/48
>>> _.evalf()
0.205616758356028
>>> mpmath.nsum(lambda k: (-1)**k / (2*k+2)**2, [0,mpmath.inf])
0.205616758356028
![\sum_{k=0}^{\infty} \frac{\left(-1\right)^{k} \left(1 + k\right)}{\left(3 + 2 k\right)^{2}} = \frac{1}{9} \,_{3}F_{2}\left(\frac{3}{2},\frac{3}{2},2; \frac{5}{2},\frac{5}{2}; -1\right) [; \sum_{k=0}^{\infty} \frac{\left(-1\right)^{k} \left(1 + k\right)}{\left(3 + 2 k\right)^{2}} = \frac{1}{9} \,_{3}F_{2}\left(\frac{3}{2},\frac{3}{2},2; \frac{5}{2},\frac{5}{2}; -1\right) ;]](http://fredrikj.net/blah/gif_021.gif)
>>> hypsum((-1)**k * (k+1) / (2*k+3)**2, k)
3F2([3/2, 3/2, 2], [5/2, 5/2], -1)/9
>>> _.evalf()
0.0652837153898853
>>> mpmath.nsum(lambda k: (-1)**k * (k+1) / (2*k+3)**2, [0,mpmath.inf])
0.0652837153898854
![\sum_{k=0}^{\infty} \frac{1}{4 + 2 k + k^{2}} = \frac{1}{6} \mathbf{\imath} \sqrt{3} \left(- \operatorname{\psi}\left(0,1 + \mathbf{\imath} \sqrt{3}\right) + \operatorname{\psi}\left(0,1 - \mathbf{\imath} \sqrt{3}\right)\right) [; \sum_{k=0}^{\infty} \frac{1}{4 + 2 k + k^{2}} = \frac{1}{6} \mathbf{\imath} \sqrt{3} \left(- \operatorname{\psi}\left(0,1 + \mathbf{\imath} \sqrt{3}\right) + \operatorname{\psi}\left(0,1 - \mathbf{\imath} \sqrt{3}\right)\right) ;]](http://fredrikj.net/blah/gif_026.gif)
>>> hypsum(1/(k**2+2*k+4), k)
I*3**(1/2)*(-polygamma(0, 1 + I*3**(1/2)) + polygamma(0, 1 - I*3**(1/2)))/6
>>> _.evalf()
0.740267076581851
>>> mpmath.nsum(lambda k: 1/(k**2+2*k+4), [0,mpmath.inf])
0.740267076581851
This work was possible thanks to the support of NSF grant DMS-0757627, which is gratefully acknowledged.
3 comments:
Very nice !
Cool. So do you plan on backporting the symbolic solver to SymPy?
Aaron: it's possible. The basic functionality anyway, it's quite simple; if I don't do it, probably someone else can do it quite easily.
Post a Comment