New mpf implementation
The mp4 branch uses a new mpf type that handles both real and complex values. It makes complex arithmetic quite a bit faster (up to twice the speed), although real arithmetic is a little slower. Some of the slowdown is due to wrapping old-format functions instead of providing new ones, so there is a bit of unnecessary overhead. The biggest advantage is not that the implementation becomes faster, but that it becomes simpler. For example, a nice feature is that complex calculations that yield real results don't need to be converted back to a real type manually. Unfortunately, writing code that also supports Python float and complex (see below) somewhat reduce the usefulness of such features.
Imaginary infinities are a little more well-behaved (i.e. j*(j*inf) gives -inf and not a complex NaN), and the representation is flexible enough that it might be possible to support unsigned infinities, infinities with an arbitrary complex sign, and possibly even zero with an arbitrary complex sign -- hey, perhaps infinities and zeros with order and residue information attached to them so you can evaluate gamma(-3)**2 / gamma(-5) / gamma(-2) directly? (Well, I'm not sure if this is actually possible, and if it is, it's probably way overkill :-)
This new implementation will not necessarily make it -- it depends on whether the pros outweigh the cons. I would very much appreciate review by others. Regardless of the outcome, writing it has been very useful for identifying and fixing problems in the interface between "low level" and "high level" code in mpmath.
This should particularly simplify the future support for a C or Cython-based backend. In fact, the current fixed-precision backend (see below) only uses about 200 lines of code -- and although it's not complete yet, it handles a large set of calculations. Adding a fast multiprecision backend based on Sage or GMPY can probably be done in an evening now. I'm not going to do such a thing right now, as I want to fix up the existing code before adding anything new; should someone else be interested though, then by all means go ahead.
I've also inserted a few other optimizations. As noted before on this blog, many of the special functions in mpmath are evaluated as linear combinations of hypergeometric series. All those functions basically fall back to a single routine which sums hypergeometric series. The mp4 branch contains a new implementation of this routine that is up to about twice as fast as before. The speed is achieved by code generation: for every different "type" (degree, parameter types) of hypergeometric series, a specialized version is generated with various bookkeeping done in advance so it doesn't have to be repeated in every iteration of the inner loop.
As an example, the following runs at 1.7x the speed:
>>> 1/timing(mpmath.hyp1f1, 1.5, 2.2, 1.35)
5620.8844813722862
>>> 1/timing(mp4.hyp1f1, 1.5, 2.2, 1.35)
9653.1737629459149
Nearly all tests pass with the new mpf type used instead of the old one -- the only significant missing piece is interval arithmetic.
Fixed-precision arithmetic
Several people have requested support for working with regular Python floats and complexes in mpmath. Often you only need a few digits of accuracy, and mpmath's multiprecision arithmetic is unnecessarily slow. Many (though not all) of the algorithms in mpmath work well in fixed precision; the main problem with supporting this feature has been that of providing an appropriate interface that avoids cluttering the code.
In the mp4 branch, this is solved by adding a fixed-precision context. This context uses the same "high-level" methods for special functions, calculus, linear algebra, etc, as the multiprecision context, while low-level functions are replaced with fixed-precision versions. For example exp is just a wrapper around math.exp and cmath.exp.
While the default multiprecision context instance is called mp, the default fixed-precision context instance is called fp. So:
>>> from mp4 import mp, fp
>>> mp.pretty = True
>>> mp.sqrt(-5); type(_)
2.23606797749979j
<class 'mp4.ctx_mp.mpf'>
>>> fp.sqrt(-5); type(_)
2.2360679774997898j
<type 'complex'>
The fixed-precision context is still missing a lot of low-level functions, so many things don't work yet. Let's try a couple of calculations that do work and see how they compare.
Lambert W function
The Lambert W function was the first nontrivial function I tried to get working, since it's very useful in fixed precision and its calculation only requires simple functions. The lambertw method is the same for mp as for fp; the latter just uses float or complex for the arithmetic.
>>> mp.lambertw(7.5)
1.56623095378239
>>> mp.lambertw(3+4j)
(1.28156180612378 + 0.533095222020971j)
>>> fp.lambertw(7.5)
1.5662309537823875
>>> fp.lambertw(3+4j)
(1.2815618061237759+0.53309522202097104j)
The fixed-precision results are very accurate, which is not surprising since the Lambert W function is implemented using a "self-correcting" convergent iteration. In fact, the multiprecision implementation could be sped up by using the fixed-precision version to generate the initial value. The speed difference is quite striking:
>>> 1/timing(mp.lambertw, 7.5)
1249.5319808144905
>>> 1/timing(mp.lambertw, 3+4j)
603.49697841726618
>>> 1/timing(fp.lambertw, 7.5)
36095.559380378654
>>> 1/timing(fp.lambertw, 3+4j)
20281.934235976787
Both the real and complex versions are about 30x faster in fixed precision.
Hurwitz zeta function
The Hurwitz zeta function is implemented mainly using Euler-Maclaurin summation. The main ingredients are Bernoulli numbers and the powers in the truncated L-series. Bernoulli numbers are cached, and can be computed relatively quickly to begin with, so they're not much to worry about. In fact, I implemented fixed-precision Bernoulli numbers by wrapping the arbitrary-precision routine for them, so they are available to full 53-bit accuracy. As it turns out, the fixed-precision evaluation achieves nearly full accuracy:
>>> mp.hurwitz(3.5, 2.25); fp.hurwitz(3.5, 2.25)
0.0890122424923889
0.089012242492388816
>>> t1=timing(mp.hurwitz,3.5,2.25); t2=timing(fp.hurwitz,3.5,2.25); 1/t1; 1/t2; t1/t2
473.66504799548278
7008.0267335004173
14.7953216374269
There is a nice 15x speedup, and it gets even better if we try complex values. Let's evaluate the the zeta function on the critical line 0.5+ti for increasing values of t:
>>> s=0.5+10j
>>> mp.hurwitz(s); fp.hurwitz(s)
(1.54489522029675 - 0.115336465271273j)
(1.5448952202967554-0.11533646527127067j)
>>> t1=timing(mp.hurwitz,s); t2=timing(fp.hurwitz,s); 1/t1; 1/t2; t1/t2
213.37891598750548
4391.4815202596583
20.580672180923461
>>> s=0.5+1000j
>>> mp.hurwitz(s); fp.hurwitz(s)
(0.356334367194396 + 0.931997831232994j)
(0.35633436719476846+0.93199783123336344j)
>>> t1=timing(mp.hurwitz,s); t2=timing(fp.hurwitz,s); 1/t1; 1/t2; t1/t2
8.1703453931669383
352.54843617352128
43.149759185011469
>>> s = 0.5+100000j
>>> mp.hurwitz(s); fp.hurwitz(s)
(1.07303201485775 + 5.7808485443635j)
(1.0730320148426455+5.7808485443942352j)
>>> t1=timing(mp.hurwitz,s); t2=timing(fp.hurwitz,s); 1/t1; 1/t2; t1/t2
0.17125208455924443
9.2754935956407891
54.162806949260492
It's definitely possible to go up to slightly larger heights still. The Euler-Maclaurin truncation in the Hurwitz zeta implementation is not really tuned, and certainly has not been tuned for fixed precision, so the speed can probably be improved.
Hypergeometric functions
Implementing hypergeometric series in fixed precision was trivial. That the multi-precision implementation is actually quite fast can be seen by comparing direct evaluations:
>>> mp.hyp1f1(2.5, 1.2, -4.5)
-0.0164674858506064
>>> fp.hyp1f1(2.5, 1.2, -4.5)
-0.016467485850591584
>>> 1/timing(mp.hyp1f1, 2.5, 1.2, -4.5)
6707.6667199744124
>>> 1/timing(fp.hyp1f1, 2.5, 1.2, -4.5)
12049.135305946565
The float version is only about twice as fast. Unfortunately, hypergeometric series suffer from catastrophic cancellation in fixed precision, as can be seen by trying a larger argument:
>>> mp.hyp1f1(2.5, 1.2, -30.5)
6.62762709628679e-5
>>> fp.hyp1f1(2.5, 1.2, -30.5)
-0.012819333651375751
Potentially, checks could be added so that the fixed-precision series raises an exception or falls back to arbitrary-precision arithmetic internally when catastrophic cancellation occurs. However, it turns out that this evaluation works for even larger arguments when the numerically stable asymptotic series kicks in:
>>> mp.hyp1f1(2.5, 1.2, -300.5)
1.79669541078302e-7
>>> fp.hyp1f1(2.5, 1.2, -300.5+0j)
1.7966954107830195e-07
The reason I used a complex argument is that the asymptotic series uses complex arithmetic internally, and Python has an annoying habit of raising exceptions when performing complex-valued operations involving floats (a proper workaround will have to be added). In this case the speedup is close to an order of magnitude:
>>> 1/timing(mp.hyp1f1, 2.5, 1.2, -300.5)
532.36666412814452
>>> 1/timing(fp.hyp1f1, 2.5, 1.2, -300.5+0j)
4629.4746136865342
Another example, a Bessel function. This function is calculated using a hypergeometric series and also a couple of additional factors, so the speedup is quite large:
>>> mp.besselk(2.5, 7.5)
0.000367862846522012
>>> fp.besselk(2.5, 7.5)
0.00036786284652201188
>>> 1/timing(mp.besselk, 2.5, 7.5)
3410.5578142787444
>>> 1/timing(fp.besselk, 2.5, 7.5)
21879.520083463747
The fixed-precision context does not yet handle cancellation of singularities in hypergeometric functions. This can be implemented as in the multiprecision case by perturbing values, although accuracy will be quite low (at best 5-6 digits; sometimes an accurate result will be impossible to obtain).
Numerical calculus
Root-finding works, as does numerical integration, with nice speedups:
>>> fp.quad(lambda x: fp.cos(x), [2, 5])
-1.8682217014888205
>>> mp.quad(lambda x: mp.cos(x), [2, 5])
-1.86822170148882
>>> 1/timing(fp.quad, lambda x: fp.cos(x), [2, 5])
1368.3622602114056
>>> 1/timing(mp.quad, lambda x: mp.cos(x), [2, 5])
55.480651962846274
>>> fp.findroot(lambda x: fp.cos(x), 2)
1.5707963267948966
>>> mp.findroot(lambda x: mp.cos(x), 2)
1.5707963267949
>>> 1/timing(fp.findroot, lambda x: fp.cos(x), 2)
19160.822293284604
>>> 1/timing(mp.findroot, lambda x: mp.cos(x), 2)
1039.4805452292442
The tests above use well-behaved object functions; some corner cases are likely fragile at this point. I also know, without having tried, that many other calculus functions utterly don't work in fixed precision (not by algorithm, nor by implementation). Some work will be needed to support them even partially. At minimum, several functions will have to be changed to use an epsilon of 10-5 or so since full 15-16-digit accuracy requires extra working precision which just isn't available.
Plotting
The plot methods work, and are of course way faster in fixed-precision mode. For your enjoyment, here is the gamma function in high resolution; the following image took only a few seconds to generate:
>>> fp.cplot(fp.gamma, points=400000)
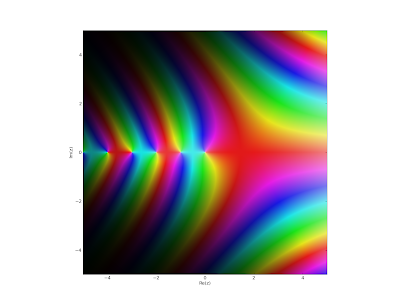
With the default number of points (fp.cplot(fp.gamma)), it's of course instantaneous.