Work has been a bit slow over the last two weeks, partially due to the fact that I was away during one of them. Nevertheless, I've been able to add a couple of more functions to mpmath, as described in the following post below. With these functions committed, I'm probably going to stop adding features and just do a new release as soon as possible (some documentation and general cleanup will be required first).
Coulomb wave functions
I have, due to a request, implemented the
Coulomb wave functions (
commit). The Coulomb wave functions are used in quantum physics; they solve the radial part of the Schrödinger equation for a particle in a 1/
r potential.
The versions in mpmath are fully general. They work not only for an arbitrarily large or small radius, but for complex values of all parameters. Some example evaluations:
>>> mp.dps = 25; mp.pretty = True
>>> coulombf(4, 2.5, 1000000)
-0.9713831935409625197404938
>>> coulombf(2+3j, 1+j, 100j)
(2.161557009297068729111076e+37 + 1.217455850269101085622437e+39j)
>>> coulombg(-3.5, 2, '1e-100')
2.746460651456730226435998e+252
The definitions of the Coulomb wave functions for complex parameters are based mostly on
this paper by N. Michel, which describes a special-purpose C++ implementation. I'm not aware of any other software that implements Coulomb wave functions, except for GSL which only supports limited domains in fixed precision.
The Coulomb wave functions are numerically difficult to calculate: the canonical representation requires complex arithmetic, and the terms vary by many orders of magnitude even for small parameter values. Arbitrary-precision arithmetic, therefore, is almost necessary even to obtain low-precision values, unless one uses much more specialized evaluation methods. The current mpmath versions are simple and robust, although they can be fairly slow in worst cases (i.e. when they need to use a high internal precision). Timings for average/good cases are in the millisecond range,
>>> timing(coulombf, 3, 2, 10)
0.0012244852348553437
>>> timing(coulombg, 3, 2, 10)
0.0068572681723514609
but they can climb up towards a second or so when large cancellations occur. Someone who needs faster Coulomb wave functions, say for a limited range of parameters, could perhaps find mpmath useful for testing a more specialized implementation against.
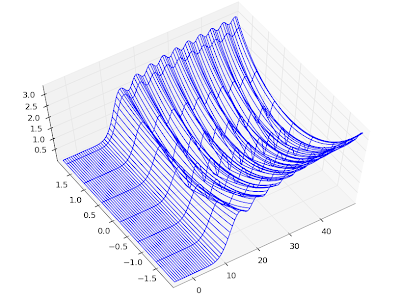
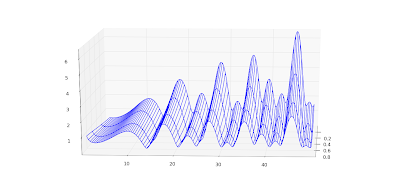
The speed is plenty for basic visualization purposes. Below I've recreated graphs 14.1, 14.2 and 14.5 from
Abramowitz & Stegun.
mp.dps = 5
# Figure 14.1
F1 = lambda x: coulombf(x,1,10)
F2 = lambda x: coulombg(x,1,10)
plot([F1,F2], [0,15], [-1.2, 1.7])
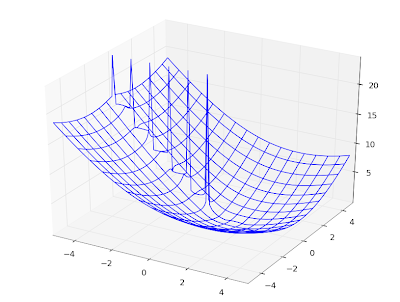
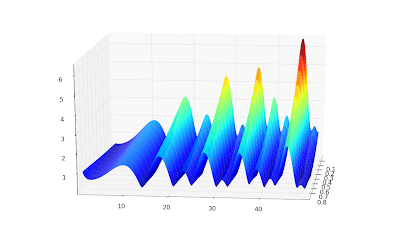
# Figure 14.3
F1 = lambda x: coulombf(0,0,x)
F2 = lambda x: coulombf(0,1,x)
F3 = lambda x: coulombf(0,5,x)
F4 = lambda x: coulombf(0,10,x)
F5 = lambda x: coulombf(0,x/2,x)
plot([F1,F2,F3,F4,F5], [0,25], [-1.2,1.6])
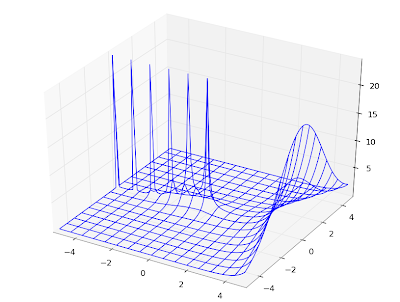
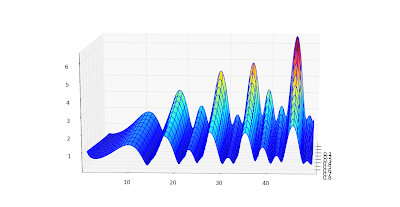
# Figure 14.5
F1 = lambda x: coulombg(0,0,x)
F2 = lambda x: coulombg(0,1,x)
F3 = lambda x: coulombg(0,5,x)
F4 = lambda x: coulombg(0,10,x)
F5 = lambda x: coulombg(0,x/2,x)
plot([F1,F2,F3,F4,F5], [0,30], [-2,2])
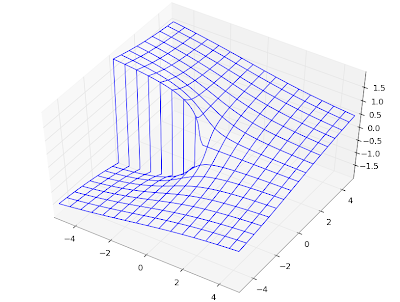
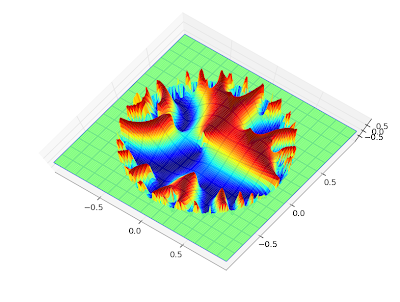
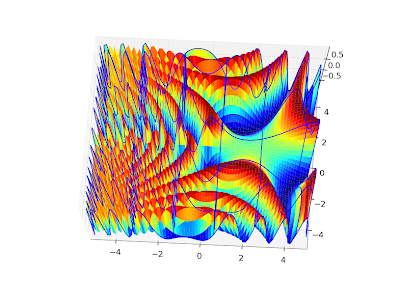
Also, a plot for complex values,
cplot(lambda z: coulombg(1+j, -0.5, z)):

Orthogonal polynomials
I've added the (associated) Legendre functions of the first and second kind, Gegenbauer, (associated) Laguerre and Hermite functions (commits
1,
2,
3,
4). This means that mpmath finally supports all the classical orthogonal polynomials. As usual, they work in generalized form, for complex values of all parameters.
A fun thing to do is to verify orthogonality of the orthogonal polynomials using numerical quadrature:
>>> mp.dps = 15
>>> chop(quad(lambda t: exp(-t)*t**2*laguerre(3,2,t)*laguerre(4,2,t), [0,inf]))
0.0
>>> chop(quad(lambda t: exp(-t**2)*hermite(3,t)*hermite(4,t), [-inf,inf]))
0.0
As another basic demonstration, here are some Legendre functions of the second kind, visualized:
F1 = lambda x: legenq(0,0,x)
F2 = lambda x: legenq(1,0,x)
F3 = lambda x: legenq(2,0,x)
F4 = lambda x: legenq(3,0,x)
F5 = lambda x: legenq(4,0,x)
plot([F1,F2,F3,F4,F5], [-1,1], [-1.3,1.3])

Implementing these functions is a lot of work, I've found. The general case is simple (just fall back to generic hypergeometric code), but the special cases (singularities, limits, asymptotically large arguments) are easy to get wrong and there are lots of them to test and document.
My general methodology is to implement the special functions as the
Wolfram Functions site defines them (if they are listed there), test my implementation against exact formulas, and then test numerical values against Mathematica. Unfortunately, Wolfram Functions often leaves limits undefined, and is not always consistent with Mathematica. In fact, Mathematica is not even consistent with itself. Consider the following:
In[277]:= LaguerreL[-1, b, z] // FunctionExpand
Out[277]= 0
In[278]:= LaguerreL[-1, -2, z] // FunctionExpand
z 2
E z
Out[278]= -----
2
It's tempting to just leave such a case undefined in mpmath and move on (and perhaps fix it later if it turns out to be used). Ideally mpmath should handle all singular cases correctly and consistently, and it should state in the documentation precisely what it will calculate for any given input so that the user doesn't have to guess. Testing and documenting special cases is very time-consuming, however, and although I'm making progress, this work is far from complete.